탐색 1

인공지능개론(정명희) 4주차 강의내용

탐색 Preview

• 인간의 공간 탐색space search 능력
  예) 축구: 점수를 올리기 위해 골을 넣는 문제 - 순간순간 공간 탐색 수행
  
  • 슛을 할지 패스를 할지, 어느 위치를 점유할지
    
• 인공지능의 공간 탐색 능력
  
  • 알파고와 알파스타
    
  • 현재 게임 상태에서 최적의 다음 상태를 탐색
    
  • 최적의 화학 구조식을 탐색

탐색과 문제 해결

• 문제해결 -> 탐색과정을 통해 문제의 해에 도달 -> 자동화된 해결방안 필요
  
• 문제해결 과정 중에 지능적 판단이 필요한 경우 탐색기법 필요
  
• 문제해결의 최적의 방법보다 적당한 방법을 찾는 것이 필요함
  
• Maximization vs. Optimization

상태 공간 탐색

• 상태공간의 도입 -> 상태공간 탐색(state space search)
  
  • 문제의 정형화에 유리
    
• 문제 정의(공식화) 5가지 요소
  ① 초기 상태
  ② 상태공간
  ③ 연산자
  ④ 목표 상태
  ⑤ 비용 함수
  
• 다양한 문제를 상태공간으로 모델링 (퍼즐, 미로, 경로 탐색 등)

상태 공간과 탐색

상태(state)

• 특정 시점에 문제의 세계가 처해 있는 모습
  
• 초기 상태(initial state)
  
  • 문제가 주어진 시점의 시작 상태
    
• 목표 상태(goal state)
  
  • 문제에서 원하는 최종 상태

탐색(search)

• 상태공간에서 시작상태에서 목표상태까지의 경로를 찾는 것

상태 공간(state space)

• 문제의 해가 될 가능성이 있는 모든 상태들의 집합
  
• 상태들이 모여 있는 공간
  
• 상태공간그래프: 상태를 노드로 표현하고 노드들 간에 간선을 추가한 그래프

상태 공간 그래프(state space graph)

• 상태공간에서 각 행동에 따른 상태의 변화를 나타낸 그래프
  
  • 노드 : 상태
    
  • 링크 : 행동
    
• 일반적인 문제에서는 상태공간이 매우 큼
  
  • 미리 상태 공간 그래프를 만들기 어려움
    
  • 탐색과정에서 그래프 생성

탐색문제 예제

• 선교사-식인종 강 건너기 문제
  
• 8-퍼즐 문제
  
• 8-퀸(queen) 문제
  
• 틱-택-토 (tic-tac-toe)
  
• 순회 판매자 문제 (traveling salesperson problem, TSP)
  
• 루빅스큐브 (Rubik’s cube)
  
• 스도쿠

상태공간 예제

• 문제 정의(공식화) 5가지 요소

1. 초기 상태 (Initial State) : 문제 시작점
   예 : 8-puzzle에서 타일이 섞여 있는 초기 보드
   
2. 상태공간 (State Space) : 가능한 모든 상태들의 집합.
   각 상태는 하나의 노드로 표현 (트리 또는 그래프)
   
3. 연산자 (Operators) : 현재 상태 → 새로운 상태로 바꾸는 규칙
   8-puzzle에서는 빈칸을 상하좌우로 움직이는 것
   
4. 목표 상태 (Goal State) : 문제의 해결 상태
   예 : 타일이 순서대로 정렬된 상태
   
5. 비용 함수 (Path Cost) : 상태 전이(transition)에 드는 비용
   예 : 한 번 움직일 때 비용 = 1 (최단 이동 횟수 찾기)

예) 8-Puzzle 문제 모델링

1. 상태공간 :
   모든 가능한 3x3 보드 배치를 노드로 생각 → 총 9! = 362,880개 상태
   (단, 실제 도달 가능한 상태는 절반 ≈ 181,440개)
   
2. 연산자 :
   
   • UP: 빈칸을 위쪽 타일과 교환
     
   • DOWN: 아래쪽과 교환
     
   • LEFT: 왼쪽과 교환
     
   • RIGHT: 오른쪽과 교환
     
3. 비용 함수 :
   
   • 각 이동의 비용 = 1
     
   • 경로 비용 = 이동 횟수 합계 → 최단 이동 경로를 찾는 것이 목표

인공지능에서의 탐색 기법

추론을 통한 탐색

• 순방향 추론과 역방향 추론이 있음
  
  • 순방향 추론은 출발 상태에서 목표 상태로 진행
    
  • 역방향 추론은 목표 상태에서 출발 상태로 진행
    
• 순방향 추론과 역방향 추론을 접합한 양방향 추론도 있음

탐색 트리 구축

• 트리 구조 그래프는 보통 출발점이 되는 정점(초기 상태)에서 다른 정점을 향해 나가는 모습(계통나무)을 통해 여러 가지를 선택할 수 있는 상태를 나타냄
  예: 체스, 오델, 미로 찾기, 대중교통 환송
  
• 출발점에서 목적지를 노드로 구성한 후 분기를 이용해 상태를 선택합니다.
  
• 탐색 트리는 노드에 이익과 비용 값을 저장해 두고 목적지에 도달하는 최적 경로를 찾음
  
• 탐색 결과를 기반으로 다음 노드 선택 시 여러 노드의 평가 값을 계산해서 최적 경로 선택 (비용함수)
  
  • Ex) 대중교통 - 출발점에서 목적지까지 다양한 대중교통수단을 이용했을 때의 최소 이동 시간， 최소 환승 횟수， 꼭 지나는 중간 지점, 환승 요금 계산
    
• 현재 시각 t에서 이익이나 지불 비용을 계산한 다음 t+1 상태 결정
  -> 과정을 반복 실행하며 목적지에 도달
  -> 이익을 최대화하거나 비용을 최소화하는 계획
  
• 목표 상태를 효율적으로 찾는 지능적인 공간 탐색 알고리즘 필요

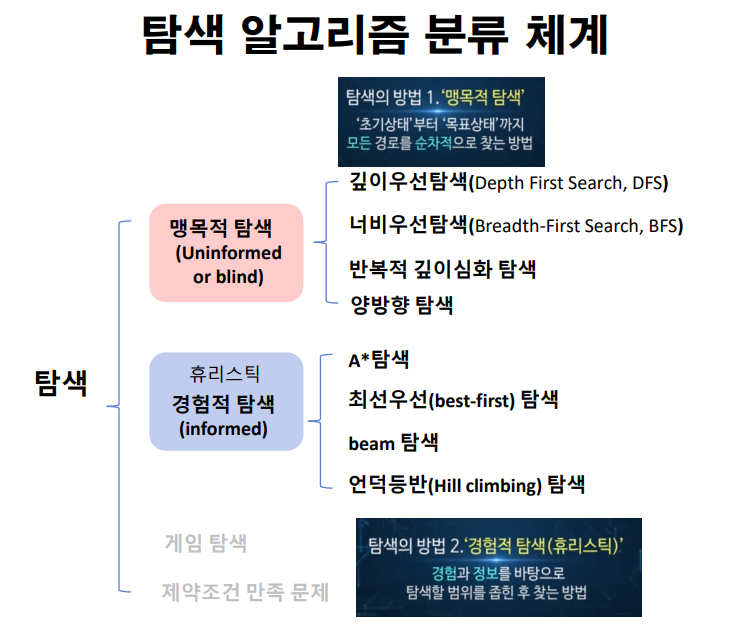
1) 맹목적(무정보) 탐색(blind search)

• 정해진 순서에 따라 상태 공간 그래프를 점차 생성해 가면서 해를 탐색하는 방법
  “효율적인 전략 없이 미리 정해 놓은 순서에 따라 탐색하는 알고리즘”

(1) 너비 우선 탐색(Breadth-First Search, BFS)
• 시작 정점 방문 후 시작 정점과 연결된 모든 정점들을 왼쪽부터 차례 대로 방문
• 그 후 level의 순서에 따라 차례로 탐색
• 즉 level 0, level 1, level 2, … 의 순서로 탐색
• 그림에서 1, 2, 3, 4, 5, 6의 순서로 방문 • Queue이용, 최적해 보장 → 메모리 많이 필요

(2) 깊이 우선 탐색(Depth First Search, DFS)
• 첫 정점(node) 방문, 왼쪽으로 이동하여 계속 탐색
• 탐색할 정점이 없으면, 되돌아와서 순환적으로 탐색
• 그림에서 1, 2, 3, 4, 5, 6의 순서로 방문
• Stack, 재귀 구현 → 장점(메모리 적음) vs 단점(최적성 X)

(3) 반복적 깊이심화(증가) 탐색(Iterative Deepening Search, IDS)
• 깊이 한계를 1씩 증가 시키며 그때마다 깊이 우선 탐색 을 반복적으로 실행 하는 알고리즘
• 반복적 깊이심화 탐색(IDS)의 작동 방식
① 깊이 1에서 시작 : 깊이 한계(depth limit)를 0으로 설정하고 깊이 우선 탐색을 실행합니다.
② 점진적 깊이 증가 : 깊이 한계를 1씩 늘려가며 각 단계마다 깊이 우선 탐색을 반복적으로 실행합니다.
③ 목표 탐색 : 목표 노드에 도달할 때까지 이 과정을 반복합니다.
• 메모리 효율과 최단경로 보장
• DFS + BFS의 장점만을 취하는 알고리즘
• 맹목적 탐색 적용시 우선 고려 대상

(4) 양방향 탐색
• 초기노드와 목적노드에서 동시에 너비 우선 탐색을 진행
• 중간에 만나도록 하여 초기 노드에서 목표 노드로의 최단 경로를 찾는 방법

• 두 개의 너비 우선 탐색(BFS)을 동시에 사용
  • 정방향 탐색 (Forward Search): 초기 노드에서부터 BFS를 시작하여 확장
  • 역방향 탐색 (Backward Search): 목표 노드에서부터 BFS를 시작하여 확장
  • 종료 조건: 두 탐색의 경계(frontier)가 서로 만나거나, 한쪽 탐색이 확장하려는 노드가 다른 쪽에서 이미 방문한 노드일 때 탐색 종료

맹목적(무정보) 탐색 정리
너비우선 탐색(BFS)은 최적의 해를 찾으나 메모리 사용이 비효율적이다.
깊이우선 탐색(DFS)은 메모리 사용이 효율적이나 최적의 해를 보장하지 못한다.
반복적 깊이우선 탐색(IDS)은 메모리 사용이 효율적이면서도 최적의 해를 보장한다.

2) 경험적(정보이용)탐색(informed search)

• 탐색시간을 줄이기 위해 문제에 관련된 정보(휴리스틱 정보)를 이용하는 탐색: “목표까지 남은 비용”에 대한 추정값(낙관적일수록 좋음)
  
• AI 탐색에서 휴리스틱 함수 h(n)은 현재 노드 n에서 목표까지 도달하는데 드는 예상 비용(estimated cost)을 계산하는 함수 사용
  
  • 실제 비용이 아닌, 추정치(estimate)
    
  • 각 노드(선택지)마다 “이 길이 얼마나 유망한가?”를 점수로 매겨, AI가 더 유망해 보이는 경로를 우선적으로 탐색하도록 유도
    
• 휴리스틱은 비슷한 문제에 대한 과거의 경험들을 바탕으로 직관적으로 판단하여 선택하는 의사결정 방식
  
• 인공지능에서 휴리스틱 알고리즘이 상당히 많이 쓰임
  
• 논리적이거나 최적의 방법을 보장하는 것은 아님
  
• 만족할만한 해결책의 비교적 빠른 실용적인 방법
  
• 현실적으로 만족할 수 있는 답을 찾는 접근법
  
• 인공지능, 심리학, 경제학 분야에서 많이 사용

(1) A* 알고리즘 (경로 탐색)
• 지식을 이용하여 탐색 진행
• ‘문제 해결에 매우 효과적인 탐색 알고리즘
• 출발점(시작)에서 목표지점(끝)까지의 최적 경로 탐색의 한 방법
• 가장 비용이 적거나 짧은 경로 찾기(전체 비용을 최소로 하는 노드 확장)
• 평가 함수 f를 사용하여 다음에 이동할 경로를 결정함
비교) 다익스트라 알고리즘 – 시작점은 있고 임의의 목표점에 대해 최단 거리 찾는 방식

휴리스틱 함수heuristic function
• 상태의 좋은 정도를 측정하는 평가 함수evaluation function
• 인공지능에서는 평가 함수를 휴리스틱 함수heuristic function라 부름
Ex) 8-puzzle 두 가지 휴리스틱 함수
① 불일치 수: 제자리에 없는 수를 셈
② 맨해튼 거리의 합: 제자리를 찾아가는데 필요한 거리의 합

• 경험적 탐색은 경험적 평가 함수 h(n)를 사용하여 목표 상태까지의 좋은 정도를 평가한다.
• 일반적으로 경험적 탐색은 최적의 해를 보장하지는 못한다.
• 그러나 A* 알고리듬은 경험적 탐색 방법임에도 불구하고, h(n)이 허용성을 만족하면 최적의 해를 보장한다.

(2) 언덕 오르기 (hill climbing)
• 현재 노드 -> 휴리스틱 평가 값이 가장 좋은 것 하나만을 선택해서 확장하는 기법
• 매 단계 가장 좋은 이웃 하나로 “오르기”; 큐/백트래킹 거의 없음(지역탐색)
• 장점: 메모리·구현 매우 단순, 매우 빠름.
• 단점: 지역 최적/평지(plateau)/능선(ridge)에 갇힘
→ 무완전, 비최적.
① 먼저 현재 위치를 기준으로 해서, 각 방향의 높이를 판단한다.(노드의 확장)
② 만일 모든 위치가 현 위치보다 낮다면 그 곳을 정상이라고 판단한다(목표상태인가의 검사).
③ 현 위치가 정상이 아니라면 확인된 위치 중 가장 높은 곳으로 이동한다(후계 노드의 선택).

(3) 최상우선 탐색 (best-first search)
• 가장 유망해 보이는 노드를 먼저 선택하여 탐색하는 방식
• 노드의 평가 함수 f(n)(유망도를 나타내는 휴리스틱 값) 값을 기준으로 우선순위 큐에서 가장 작은 값을 가진 노드를 꺼내 확장

알고리즘 :
① 시작 노드를 f(start) 값으로 우선순위 큐에 넣음
② 큐가 빌 때까지 반복:
• f(n)이 가장 작은 노드를 꺼냄
• 목표라면 경로 반환
• 이웃 노드 생성 후 f(n) 계산 → 큐에 추가
③ 큐가 비면 해 없음

f(n)에 따라 다양한 변형 가능:
• Greedy Best-First: f(n)=h(n) → 순수 휴리스틱 기반, 빠르지만 최적해 보장 X
• A* 탐색: f(n)=g(n)+h(n) → 경로비용+휴리스틱, h가 허용적(admissible)이면 최적해 보장

• 최상우선탐색은 A* 탐색 알고리즘 과정과 유사
• 차이점은 노드의 값을 계산하는 방식
• 최상우선탐색 - 현재 노드로부터 목표 노드까지의 거리 (휴리스틱 목적함수)
• A* 탐색 - (출발 노드 ~ 현재 노드까지의 거리) + (현재 노드~목표 노드까지의 예상 거리)