탐색 2
인공지능개론(정명희) 5주차 강의내용
인공지능에서의 탐색 기법
– 맹목적 탐색
– 정보이용 탐색
– 게임에서의 탐색 –> 적대적탐색(Adversarial Search)
게임 탐색
• 두 명 이상의 플레이어가 교대로 움직이는 환경에서, 최적의 수를 찾는 탐색 과정
• 예시: 체스, 바둑, 틱택토(Tic-Tac-Toe)
• 목표: 상대가 최선의 수를 둔다고 가정했을 때, 최선의 전략을 선택
Game Tree (게임 트리) 용어
• 노드(Node): 게임 상태 (예: 보드판 배치)
• 간선(Edge): 플레이어의 수(move)
• 루트(Root): 초기 상태
• 리프(Leaf): 게임 종료 상태 (승/패/무승부)
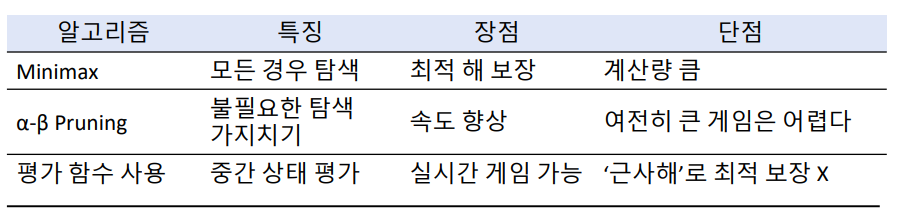
게임에서의 탐색 알고리즘
• Minimax 알고리즘(mini-max algorithm)
• α-β 가지치기 (prunning)
• 몬테카를로 트리 탐색(Monte Carlo Tree Search, MCTS)
적대적 탐색
“두개의 에이전트가 적대적 관계를 가질 때의 탐색”
1) Minimax 알고리즘(mini-max algorithm)
• 두 사람이 번갈아 수를 두고 승패를 겨루는 게임으로 확장
– 체스와 바둑 등
– 새로운 탐색 알고리즘 필요
– 인공지능은 어떤 전략을 구사해 상대를 이길 수 있을까?
• 미니맥스 핵심 전략
– MAX Player: 자신의 이득을 최대화하려고 함
– MIN Player: 상대의 이득을 최소화하려고 함 (상대 차례에서는 min을 적용, 상대의 최적의 수는 나에게 최악의 수이므로 min 적용)
– Minimax 값: 리프 노드의 점수를 위로 전파하여, 양쪽 모두 최적의 전략을 따른다고 가정했을 때의 결과
2) α-β 가지치기 (prunning)
Minimax의 불필요한 가지 탐색을 줄이는 방법
• Alpha (α): MAX가 지금까지 확보한 최선의 값 (하한선)
• Beta (β): MIN이 지금까지 확보한 최선의 값 (상한선)
• 가지치기 규칙 :
어떤 노드의 값이 α ≥ β가 되면, 더 이상 탐색할 필요 없음
Minimax을 개선한 적대적 탐색방법으로서, Max가 찾아 놓은 최선값인 알파값 (or Min이 찾아 놓은 최선값인 베타값)을 유지하여 후보 노드의 좋은 정도가 알파값보다 작을 경우 (or 베타값보다 클 경우) 가지치기를 함으로써 보다 효율적인 탐색 수행
장점
• Minimax와 동일한 결과 보장
• 탐색해야 할 노드 수를 절반 이상 줄일 수 있음
• 큰 게임(체스, 바둑)에서도 실질적으로 사용 가능한 탐색 방법
Monte Carlo Tree Search (MCTS)
• 정의:
게임 트리 탐색에서 Monte Carlo 시뮬레이션을 이용해 유망한 수를 평가하는 탐색 기법
Monte Carlo(임의, random ) + tree search
– 무작위 시뮬레이션(랜덤 플레이아웃)을 수없이 반복하여 특정 수가 얼마나 승리할 확률이 높은지를 근사적으로 계산(랜덤으로 게임을 끝까지 진행해보고, 그 승패 결과를 바탕으로 현재 수의 가치를 판단)
• 사용 분야:
– 게임 AI (특히 바둑, 체스, 퍼즐, 강화학습)
– Google DeepMind의 AlphaGo 핵심 알고리즘
• 장점:
– 평가 함수 없이도 동작 가능
– 탐색과 확률적 평가를 결합
– 게임 상태 공간이 큰 경우 효과적
• UCT(Upper Confidence bounds applied to Trees) 알고리즘
– 핵심적으로 사용되는 함수가 바로 UCB1(Upper Confidence Bound 1)
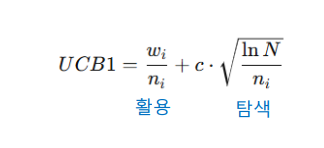
wi: i번째 자식 노드의 승리 횟수
ni: i번째 자식 노드의 총 방문(시뮬레이션) 횟수
N: 부모 노드의 총 방문(시뮬레이션) 횟수
c: 탐색의 비중을 조절하는 상수 (보통 루트2 사용)
• UCB1 값을 계산하여 이 값이 가장 높은 노드를 계속 선택
-> 탐색(Explore)과 활용(Exploit)의 균형을 수학적으로 조정
-> 현재까지 가장 승률이 좋았던 길을 선택하는 경향(활용)과 아직 시도해 보지 않은 새로운 길을 탐험하려는 경향(탐색) 사이에서 균형적 학습
예제: 최고의 광고 배너 찾기
• 웹사이트에 3가지 광고 배너(Banner A, Banner B, Banner C)를 띄운다고 가정
Q. 어떤 배너가 사용자들에게 가장 클릭률(CTR)이 높은(가장 좋은) 배너인지를 효율적으로 찾아내고자 한다.
목표: 총 1000명의 방문자에게 광고를 보여줄 예정인데, 가장 높은 클릭률을 가진 배너를 찾아 최대한 많은 클릭을 얻는 것

• MCTS 4단계 알고리즘:
1 - Selection (선택) – 트리에서 promising node 선택
2 - Expansion (확장) – 새로운 노드를 확장
3 - Simulation (Rollout, 시뮬레이션) – 랜덤 플레이아웃으로 결과 시뮬레이션
4 - Backpropagation (역전파) – 결과를 부모 노드로 전파하여 가치 업데이트
인공지능과 관련된 흥미로운 문제들
제약조건 만족 문제
(1) 인공지능 문제 해결을 위한 중요 단계
• 문제를 명확하게 정의
• 문제에 대한 철저한 분석
• 정해진 제약 조건이나 규칙이 있는 경우 규칙의 적용에 대한 검증
• 최적의 기법 선택
• 결과가 나오면 과정에 문제점이 없는지 분석 검토
(2) 초기의 인공지능 적용 문제 ‘상자 쌓기’
• 일정한 규칙과 목표 상태가 주어진 경우 인공지능을 이용하여 해결하는 방법의 예
[문제] 상자 쌓기 문제
• 왼쪽에서 상자를 하나씩 옮겨 목표 상태로 만들기
• 작은 번호의 상자가 큰 번호 상자 밑으로 가도록 함
• 상자는 다른 상자 위나 바닥 C에 놓을 수 있음
• 상자의 이동 횟수와 그 방법?

상자 쌓기 문제의 인공지능적인 풀이
• 규칙기반 시스템의 지식베이스와 추론규칙을 만들어 적용
• A 위에는 1, 3이 차례로 있고, B 위에는 2가 있음
C 위에는 아무 것도 없는 사실을 지식베이스에 저장
• 여기서의 추론규칙은 “상자를 하나씩 옮긴다.”와 작은 번호의 상자가 큰 번호의 상자 밑으로 가도록 하려고 한다.”
• 목표 상태는 “A 위에 1, 2, 3이 차례대로 놓인다.”
• 규칙기반 인공지능 프로그래밍 언어를 사용하여 해결
(3) ‘8-puzzle 게임’
• 인공지능에서 휴리스틱을 사용하는 초기의 예
• 3 × 3 크기의 박스에서 목표 상태로 가는 게임
• 게임 판의 숫자는 빈칸을 향해 상하좌우로 움직임
• 미국 유치원과 초등학생들의 두뇌 향상 게임
• 생각보다 오래 걸리는 경우가 있음
‘8-puzzle 게임’의 휴리스틱
• 이 문제를 푸는 휴리스틱은 무엇일까?
• 위치가 맞지 않은 숫자의 개수를 줄여나가는 방향으로 이동
(즉, 위치가 맞는 개수를 늘려나가는 방향)
• 최종적으로 8개의 위치를 모두 일치시키기
(4) ‘물통 문제’
물통(water jug 또는 물주전자) 문제
• 주어진 사실과 규칙들을 적용하여 문제를 해결
• 4리터짜리와 3리터짜리 물통이 각각 하나씩 있음
• 물통들에는 용량을 나타내는 어떠한 표시도 없음
• 4리터짜리 물통에다 꼭 2리터의 물을 채우는 방법?
사용할 수 있는 몇 가지 규칙이나 동작
• 물통에 물을 가득 채우기
• 물통의 물을 전부 다 비우기
• 물통에 남은 물을 다른 물통에다 붓기
• 물통의 물을 다른 물통이 가득 찰 때까지 붓기
(5) 문자 암호 풀이
• 1824년 퍼즐왕 헨리 듀드니의 유명한 문자 문제
• 뉴웰(Newell)에 의해 채택된 초기의 인공지능 문제
• 정교한 인공지능 프로그램을 통해 해결한 예
[문제] 각 문자는 0에서 9까지의 각각 다른 숫자 가짐
각 문자에 해당하는 숫자 구하기

(6) 규칙의 적용을 이용한 문제 해결
[문제 1] 늑대, 염소, 양배추 문제
• 사람이 늑대, 염소, 양배추와 강의 오른쪽에 있음
• 사람은 이 중 하나만 선택, 강의 왼쪽/오른쪽으로 이동
• 사람 혼자서 건널 수도 있음
• 늑대와 염소만 남겨 두면 늑대가 염소를 잡아먹음
• 염소와 양배추만 남겨 두면 염소가 양배추를 먹음
• 염소나 양배추가 먹히지 않고 모두 강을 건너는 방법?

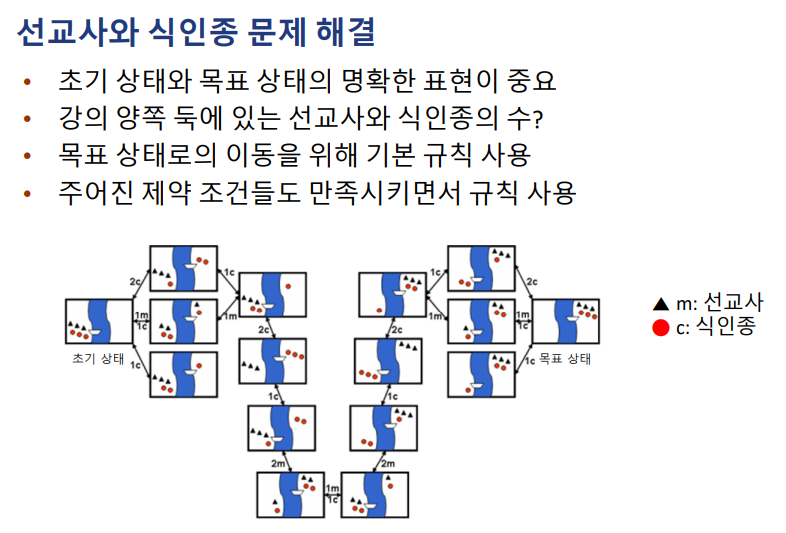
[문제 2] ‘선교사와 식인종’ 문제
• 3명의 선교사, 3명의 식인종, 배 1척이 왼쪽에 위치
• 목표는 선교사와 식인종 모두 배를 타고 강을 건넘
• 어떤 방법으로 모두 건널 수 있는가?
이동의 제약 조건
• 배에는 최대 2명까지 탈 수 있음
• 선교사와 식인종 누구나 배 조종 가능
• 식인종 수 > 선교사 수, 식인종이 선교사 해침
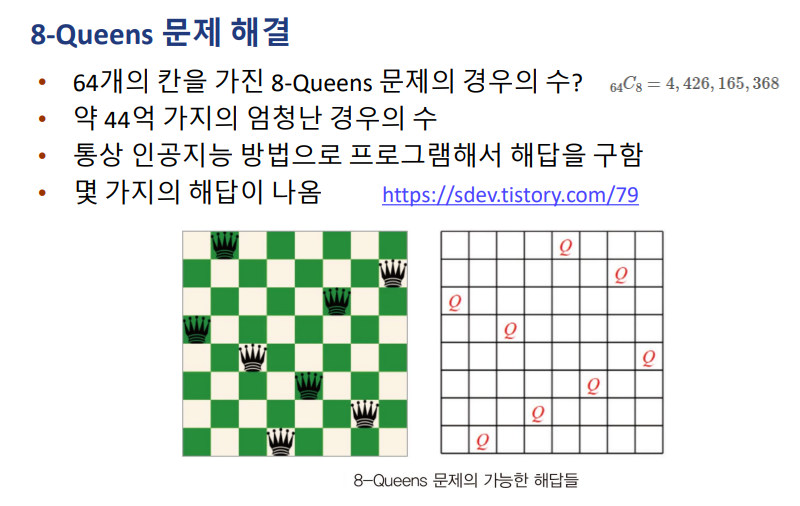
8-Queens 문제
• 8-Queens 문제는 체스에서 유래
• 서로를 공격하지 않는 위치에 8개의 퀸(Q) 배치
• 퀸은 수평, 수직, 대각선 방향으로 몇 칸이든 이동 가능
• 어떤 퀸도 서로 공격 당하지 않는 위치에 놓여야 함
4-Queens 문제
• 체스 판을 4 x 4로 축소한 소위 4-Queens 문제
• 2가지 경우의 해답을 얻을 수 있음
• 수평, 수직, 대각선 방향으로 점검
• 어떤 퀸도 서로 공격 당하지 않는 위치임을 확인
