K-NN
인공지능개론(정명희) 9주차 강의내용
K-Nearest Neighbor(K-NN)
- 간단한 분류 기법, ‘최근접 이웃 분류’라고도 불림
- 새로운 입력 데이터와 가장 가까운 k개의 이웃 데이터 선택
- 이웃 데이터들의 클래스 중 다수결로 데이터의 클래스 결정
- 다수결에서 결과가 나오기 위해 k는 반드시 홀수여야 함
거리 계산 방법
- 유클리드 거리(Euclidean distance)
두 지점 간의 직선 거리 - 맨하탄 거리(Manhattan distance)
격자 형태(바둑판)의 두 지점 간 거리 - 코사인 유사도(cosine similarity)
두 벡터 간의 각도 - 민코브스키 거리(Minkowski distance)
차수(r)가 1이면 맨하탄 거리,
차수가 2이면 유클리드 거리
작동 원리 (4단계)
- k값 설정 : 몇 개의 이웃을 참고할지 결정한다.
- 거리 계산 : 새로운 데이터와 모든 기존 데이터 사이의 거리를 계산한다.
- 이웃 찾기 : 계산된 거리상 가장 가까운 k개의 이웃을 찾는다.
- 분류 결정 : 가장 많은 표를 받은 클래스로 새로운 데이터를 결정한다. (다수결 투표)
| 파라미터 | 설명 | 영향 |
|---|---|---|
| k (이웃의 수) | 투표에 참여할 이웃의 개수 | k가 작으면 민감(과적합), 크면 일반화(과소적합) |
| 거리 척도 (Metric) | 유사도 계산 방법 | 기본은 유클리드 거리 |
| 가중치 (Weights) | '균등' 또는 '거리 기반' 가중치 적용 | 가까운 점에 더 큰 영향 부여 가능 |
| 탐색 알고리즘 | brute, kd_tree, ball_tree | 속도 및 메모리 효율에 영향 |
| 장점 | 단점 |
|---|---|
| 구현이 간단하고 직관적 | 대규모 데이터에서 느림 (모든 거리 계산 필요) |
| 학습 과정이 없음 (Lazy Learner) | 특성 스케일링에 민감 |
| 다중 클래스 문제도 자연스럽게 해결 | 명시적 모델이 없어 해석 어려움 |
| 데이터 분포가 명확할 때 성능 우수 | 고차원 데이터에서는 성능 저하 (차원의 저주) |
| 분야 | 예시 | 목적 |
|---|---|---|
| 의료 | 환자 증상으로 질병 예측 | 분류 |
| 금융 | 대출 신청자 부도 여부 예측 | 분류 |
| 전자상거래 | 유사 상품 추천 | 분류/회귀 |
| 환경 | 센서 데이터를 이용한 오염도 예측 | 회귀 |
단계별 K-NN 실습 예제
- 5개의 표본
- 입력변수(X1, X2) 와 클래스 정보를 담고 있는 라벨인 출력 변수(Y)로 구성
- 새로운 개체인 6번째 개체의 분류 문제
| ID | X1 | X2 | Y |
|---|---|---|---|
| 1 | 25 | 25 | A |
| 2 | 33 | 30 | A |
| 3 | 38 | 30 | B |
| 4 | 45 | 35 | B |
| 5 | 28 | 40 | A |
| ID | X1 | X2 | Y |
|---|---|---|---|
| 6 | 30 | 35 | ? |
① k의 수 결정
- K = 3
- 이진 분류인 경우, K의 수는 동점을 피하기 위해 홀수로 정함
- 최적의 K : K의 변화에 따른 기존 개체들의 오분류 수를 파악하는 교차검증을 통해 결정할 수 있음
② 피처 스케일링
- 파이썬 표준화 패키지와의 일관성을 위해 모표준편차를 사용
| ID | 원 데이터 | 표준화된 데이터 | ||
|---|---|---|---|---|
| X1 | X2 | Z1 | Z2 | |
| 1 | 25 | 25 | -1.2327 | -1.3728 |
| 2 | 33 | 30 | -0.1121 | -0.3922 |
| 3 | 38 | 30 | 0.5883 | -0.3922 |
| 4 | 45 | 35 | 1.5689 | 0.5883 |
| 5 | 28 | 40 | -0.8125 | 1.5689 |
| 평균 | 33.8 | 32 | ||
| 표준편차 | 7.1 | 5.1 | ||
- Feature scaling:
머신러닝 모델의 학습 성능을 향상시키기 위해 데이터의 범위를 일정하게 맞춤 - 변수 값의 단위나 범위 차이로 인해 생길 수 있는 문제를 예방할 수 있다
| ID | 원 데이터 | 표준화된 데이터 | ||
|---|---|---|---|---|
| X1 | X2 | Z1 | Z2 | |
| 6 | 30 | 35 | -0.5323 | 0.5883 |
- 새로운 개체(테스트용)는 기존 개체(학습용)의 평균과 표준편차를 이용한 표준화
③ 유사도 측정
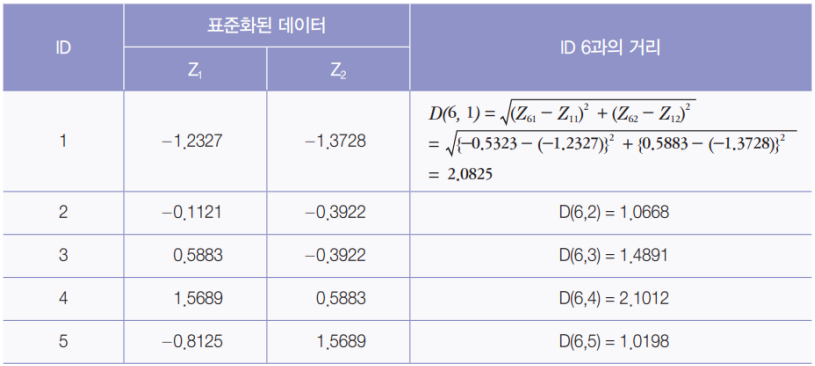
④ 최근접 이웃 선택
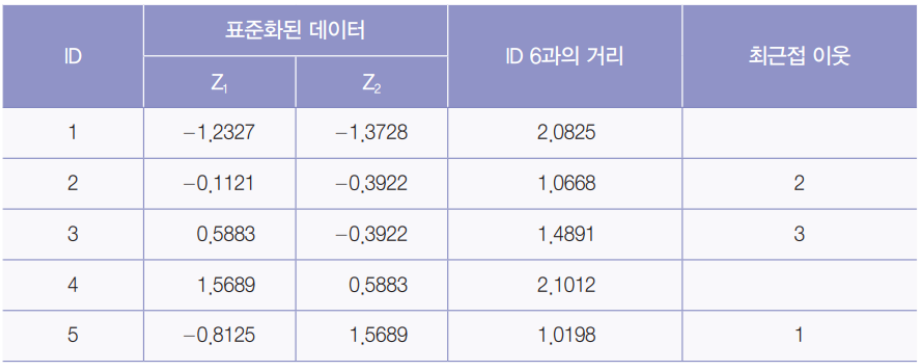
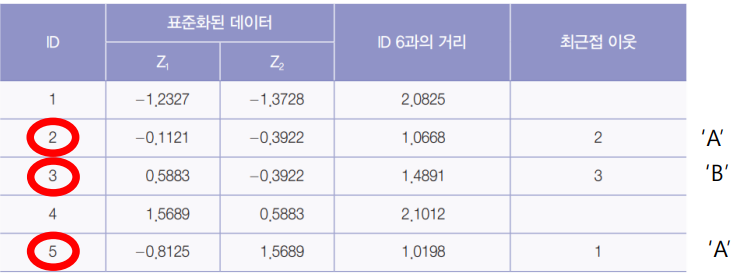
⑤ 예측
- 최근접 이웃으로 선택된 2, 3, 5는 ‘A’, ‘B’, ‘A’이기 때문에, 새로운 개체를 분류 수가 많은 ‘A’로 분류
- Y 값이 정량적인 데이터인 회귀문제의 경우, 선택된 유사 개체들의 Y 변수의 평균 값으로 새로운 개체의 값을 예측할 수 있음
위 예제의 Python 전체 코드
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
import numpy as np
import matplotlib.pyplot as plt
# 기존 개체
X_train = np.array([[25, 25], [33, 30], [38, 30], [45, 35], [28, 40]])
y_train = np.array([0, 0, 1, 1, 0])
# 새로운 개체
X_test = np.array([[30, 35]])
# 산포도 출력
plt.scatter(X_train[:, 0], X_train[:, 1], c = y_train)
plt.scatter(X_test[:, 0], X_test[:, 1], c = 'red', marker = 'D', s = 100)
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
# 피처 스케일링
scalerX = StandardScaler()
scalerX.fit(X_train)
X_train_std = scalerX.transform(X_train)
print(X_train_std)
X_test_std = scalerX.transform(X_test)
print(X_test_std)
# 모형화(디폴트 : 유클리드)
knn = KNeighborsClassifier(n_neighbors = 3, metric = 'euclidean')
# 학습
knn.fit(X_train_std, y_train)
# 예측
pred = knn.predict(X_test_std)
print(pred)
# 클래스별 확률 값을 반환
knn.predict_proba(X_test_std)
# 인접한 K개의 개체들에 대한 거리와 색인 반환
dist, index = knn.kneighbors(X_test_std)
print(dist)
print(index)
K-NN의 장단점과 활용 분야
- 장점
매우 간단하며 빠르고 효과적인 알고리즘
또 어떤 데이터라도 유사성 측정 가능 - 단점
적절한 k를 선택해야 한다는 점
새로운 데이터에 대해 일일이 거리를 계산한 후 분류 - K-NN의 활용 분야
• 영화나 음악 추천에 대한 개인별 선호 예측
• 수표에 적힌 광학 숫자와 글자인식
• 얼굴인식과 같은 컴퓨터 비전
• 유방암 등 질병의 진단과 유전자 데이터 인식
• 재정적인 위험성의 파악과 관리, 주식 시장 예측
K-NN 알고리즘 실습
K-NN의 꽃잎 분류에의 적용 예
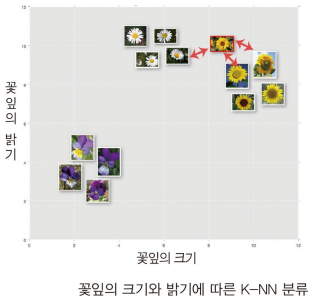
- 꽃잎의 크기와 밝기에 따른 K-NN 분류
- sklearn 라이브러리에 포함된 아이리스 데이터 세트를 활용
- 오른쪽 위에 새로운 꽃잎이 입력으로 들어왔을 때
빨간 화살표의 3가지를 비교한 후 분류하는 것을 보여줌
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
# 데이터 로드
iris = load_iris()
# 데이터(150개)
X = iris.data
# 꽃의 종류 (0 = setosa, 1=versicolor, 2=virginica)
y = iris.target
# 80 : 20으로 분할
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=4)
# K값을 7로 두고 시행
knn = KNeighborsClassifier(n_neighbors=7)
knn.fit(X_train, y_train)
# 20%의 종류 예측
y_pred = knn.predict(X_test)
# 정확도 반환
scores = metrics.accuracy_score(y_test, y_pred)
print(scores)
결과 : 0.9666666666666667 (96.7%)
classes = {0:'setosa',1:'versicolor',2:'virginica'}
# 새로운 데이터 제시
x_new = [[3,4,5,2], [5,4,2,2]]
y_predict = knn.predict(x_new)
print(classes[y_predict[0]])
print(classes[y_predict[1]])
결과 :
versicolor
setosa
K-NN의 MNIST 손글씨 데이터 적용 예
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
# 데이터 로드
mnist = fetch_openml('mnist_784', version = 1)
X, y = mnist.data / 255.0, mnist.target.astype(int)
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y,;
test_size = 0.1, random_state = 42)
# K-NN 모델 학습
knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train, y_train)
# 예측 및 정확도 평가
y_pred = knn.predict(X_test)
print(accuracy_score(y_test, y_pred))
