Decision Tree, Random Forest

인공지능개론(정명희) 11주차 강의내용

의사결정트리(Decision Tree)

정의 : 데이터를 조건에 따라 분류하거나 예측하기 위해, 트리(tree) 구조를 사용하는 알고리즘
형태 : 질문(조건)을 기준으로 데이터를 분할해 나가며, 마지막에는 결과(클래스 또는 숫자)를 예측
활용 분야 : 분류(Classification) + 회귀(Regression) 모두 가능
장점 : 직관적이고 이해하기 쉬움, 시각화 가능, 데이터 스케일 조정 불필요
단점 : 과적합(overfitting) 위험, 작은 변화에도 결과가 크게 달라질 수 있음

주요 구성 요소 :

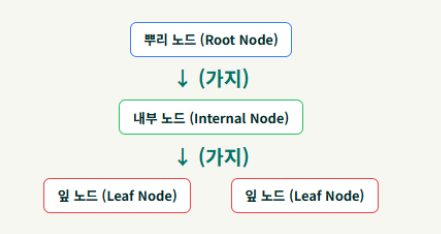
• 뿌리 노드(Root Node) : 트리의 시작점. (전체 데이터셋)
• 가지(Branch) : 노드에서 다음 노드로 이어지는 연결선 (특정 질문에 대한 결과)
• 내부 노드(Internal Node) : 뿌리 노드를 제외한, 가지가 뻗어가는 중간 노드들(질문 포함)
• 잎 노드(Leaf Node / Terminal Node) : 더 이상 분할되지 않고 최종적인 결정을 담고 있는 노드

작동 원리 :

• 데이터를 분석하여 이들 사이에 존재하는 패턴을 예측 가능한 규칙들의 조합으로 나타냄
  
• 한번에 하나씩의 설명변수를 사용하여 예측 가능한 규칙들의 집합을 생성하는 알고리즘

1. 데이터를 보고 가장 중요한 질문(특성)을 선택
2. 답(Yes/No, 숫자 범위)에 따라 데이터를 두 그룹으로 분리
3. 다시 다음 질문을 선택하고 분리 → 반복
4. 더 이상 나눌 수 없거나 결과가 동일하면 리프 노드(leaf node) 생성
   
   

결정트리 구축

• 각 노드에서 테스트할 특성 선택
  • 분류할 때 가장 유용한 특성 순서대로 선택
• 정보획득이 많은 방향으로 선택
  • 분류할 때 예제들을 얼만큼 잘 분류할 수 있는가를 측정하는 기준 필요
  • 트리구축 과정에서 테스트할 후보 특성의 순서를 결정할 때 사용
    
    

결정트리 학습의 목표
“같은 특성을 가진 데이터끼리 모이도록” 데이터를 분할해 나간다.
-> 데이터를 나눌수록 각 그룹이 하나의 클래스로만 구성되는 ‘순수한’ 상태가 되는 것이 목표

• 순도(homogeneity) 증가
  • 각 노드에 ‘같은 클래스(Label)’의 데이터만 모여 있는 상태를 지향
• 불순도 (Impurity) 감소
  • 데이터가 얼마나 섞여 있는지(불확실성)를 측정하고, 이 값을 가장 크게 줄이는 방향으로 분할

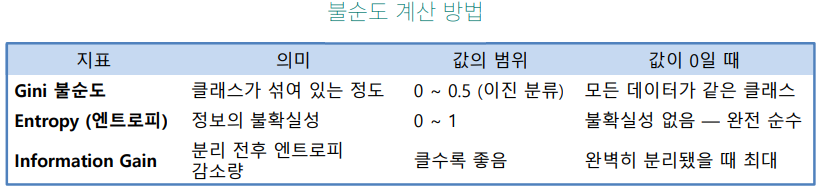
결정트리 구축 기준

• 엔트로피(Entropy)와 정보이득(획득)(Information Gain)을 기준으로 “가장 좋은 질문” 선택

\[\text{Information Gain} = \text{원래 엔트로피} - \sum \left( \frac{n_{child}}{n_{total}} \times \text{자식 노드의 엔트로피} \right)\]

1 현재 데이터가 얼마나 섞여 있는지 엔트로피(Entropy) 계산
2 각 특징(날씨, 온도, 습도 등)으로 나눴을 때의 엔트로피 변화량 계산
3 엔트로피를 가장 많이 줄여주는 특징 = 정보이득이 가장 큰 특징 선택
4 그 특징이 첫 번째 질문(루트 노드)이 된다
5 남은 데이터에 대해 같은 방식 반복 → 중간 노드/리프 노드 생성

엔트로피(Entropy) : 확률변수의 불확실성을 수치로 나타낸 것

\[I = -\sum_c p(c) \log_2 p(c)\]

• 동질인 정도 측정 가능 척도(impurity)
• 불순도를 표현하는 일반적인 방법
• 엔트로피 = 0 : 하나의 상태만으로 되는 경우
  • 무질서도가 가장 낮은 상태
• 엔트로피 = 1 : 여러 상태가 같은 비율로 섞여 있는 경우
  • 무질서도가 가장 높은 상태
    
    

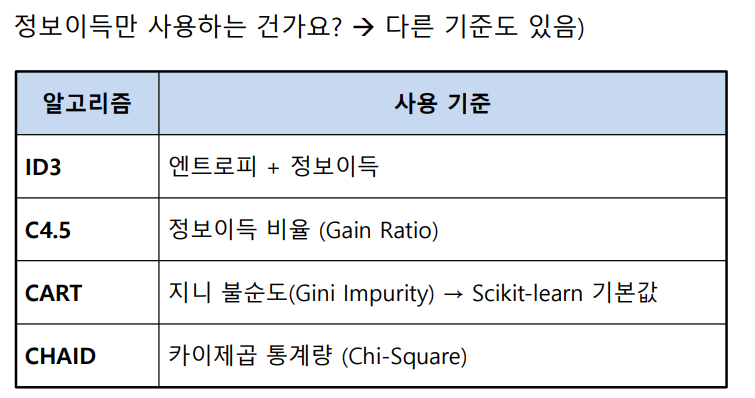
정보획득량(Information Gain)

• 원래의 엔트로피와 세부 클래스로 분할된 후의 엔트로피의 차이
• information Gain이 클수록 분류하기 좋다는 것을 의미

\[Gain(T, X) = \text{Entropy}(T) - \text{Entropy}(T, x)\] \[Entropy(T, X) = \sum P(i)E(i)\]

결정트리의 절차

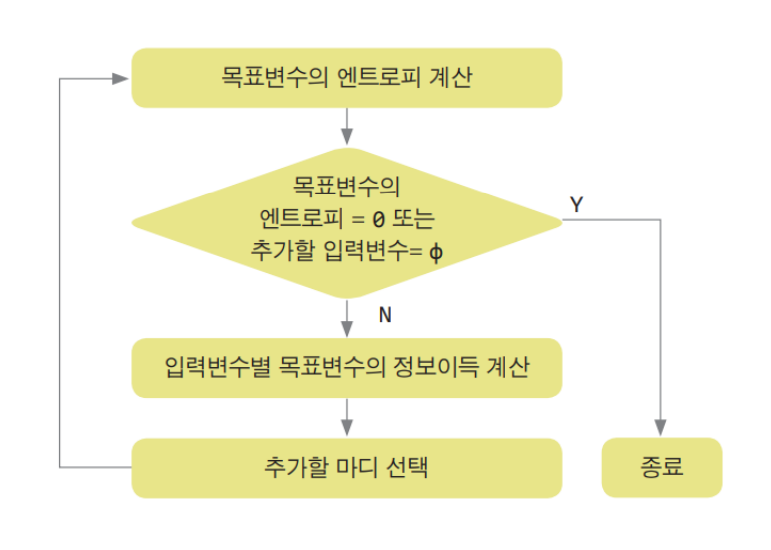
장단점

• 장점

  1. 결과를 해석하고 이해하기 쉽다.간략한 설명만으로 결정 트리 이해할 수 있다.
  2. 자료를 가공할 필요가 거의 없다. (다른 기법들의 경우 자료를 정규화하거나 임의의 변수를 생성하거나 값이 없는 변수를 제거해야 하는 경우가 있다.)
  3. 수치 자료와 범주 자료 모두에 적용할 수 있다.
  4. 비선형 관계 포착: 데이터 간의 복잡하고 비선형적인 관계를 잘 찾아낸다.

• 한계

  1. 휴리스틱 기법을 기반하기 때문에 최적 결정트리라고 보장할 수 없다.
  2. 너무 복잡한 결정트리를 만들 수 있다.
  3. 약간의 차이에 따라 (레코드의 개수의 약간의 차이) 트리의 모양이 많이 달라질 수 있다. 두 변수가 비슷한 수준의 정보력을 갖는다고 했을 때, 약간의 차이에 의해 다른 변수가 선택되면 이 후의 트리 구성이 크게 달라질 수 있다.
     
     

활용 분야

• 의학 진단 : 환자의 증상에 따라 질병 분류
• 고객 이탈 예측 : 고객의 행동 데이터를 분석하여 이탈 가능성이 있는 고객 식별
• 대출 심사 : 신청자의 정보를 바탕으로 대출 승인 여부 결정
• 텍스트 분류 : 문서의 특징(단어)에 따라 문서의 주제나 감성 분류
• 금융 예측 : 주식 시장의 흐름이나 특정 주식의 가격 변동 예측
  
  
  

랜덤 포레스트(Random Forest)

• 여러 개의 결정트리를 모아(=Forest) 다수결 또는 평균으로 예측하는 모델
  • 각 트리는 서로 다른 데이터와 특성(feature)을 보고 학습
  • 최종 예측은 “투표(Voting)” 또는 “평균(Averaging)”으로 결정
• 결정트리가 한 명의 전문가라면 랜덤 포레스트는 여러 전문가의 회의

작동 방식

1. 데이터 랜덤 추출(Bootstrap)
   전체 데이터 중 일부를 복원추출하여 트리마다 다른 데이터를 학습
2. 랜덤하게 특성 선택(Feature Randomness)
   노드를 분할할 때 모든 특성을 보는 것이 아니라 일부만 랜덤 선택
3. 트리 여러 개 생성
   각기 다른 데이터 + 특성으로 트리 생성
4. 최종 예측
   분류 : 다수결 투표
   회귀 : 평균값 사용
   
   

장단점

• 장점

  1. 높은 정확도
  2. 과적합 감소
  3. 데이터 전처리(스케일링) 거의 필요 없음
  4. 특성 중요도 확인 가능

• 한계

  1. 결정트리보다 느릴 수 있음
  2. 직관적인 해석은 어려움
  3. 트리가 많을수록 메모리 사용량 증가