비지도학습 - Clustering
인공지능개론(정명희) 11주차 강의내용
주요 비지도 학습(Unsupervised Learning) 방법
- 군집clustering
- k-평균k-Means
- 계층 군집 분석Hierarchical Cluster Analysis (HCA)
- 기댓값 최대화Expectation Maximization
- 시각화visualization와 차원 축소dimensionality reduction
- 주성분 분석Principal Component Analysis (PCA)
- 커널kernel PCA
- 지역적 선형 임베딩Locally-Linear Embedding (LLE)
- t-SNEt-distributed Stochastic Neighbor Embedding
- 연관 규칙 학습Association rule learning
- 어프라이어리Apriori
- 추천 시스템 등
군집화(Clustering)
비지도 학습 기법으로, 비슷한 데이터들을 그룹(클러스터)으로 자동 분류하는 방법
레이블 없이(unlabeled) 데이터의 자연스러운 묶음을 찾는 방법
목적 : 군집 내 유사성 최대화, 군집 간 유사성 최소화
입력 : 정답(라벨)이 없는 데이터
출력 : 각 데이터가 속하는 그룹(클러스터) 정보
필요한 이유
- 숨겨진 데이터 구조 파악
- 고차원 데이터를 단순화 및 시각화
- 전처리 및 특성 추출 단계에서 활용
- 그룹 기반 의사결정 및 전략 수립 가능
활용 분야
- 생물학 분야 : 형태 또는 유전자의 유사성으로 종과 속을 분류
- 의료분야 : 단층촬영의 3 차원 이미지에서 여러 유형의 조직을 구별
- 이미지 인식 : 손으로 쓴 숫자 이미지나 패션 이미지들을 여러 그룹으로 분류
- 고객 분류 : 고객의 취향에 따라 영화나 책을 추천하는 추천시스템에 사용
군집화의 종류
- 분할 기반 클러스터링 (Partition-Based)
- 계층적 클러스터링 (Hierarchical)

- 밀도 기반 클러스터링 (Density-Based)

- 모델 기반 클러스터링 (Model-Based)

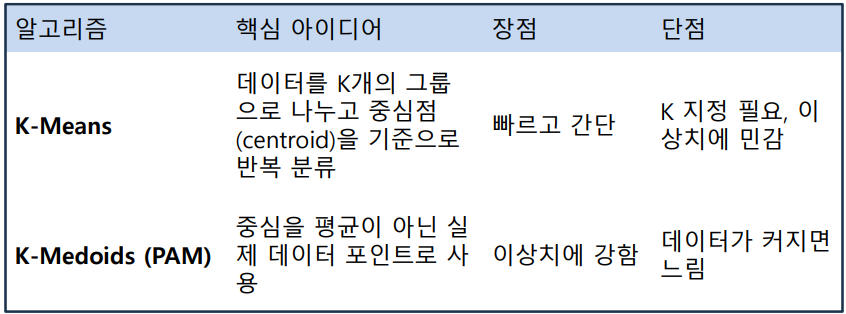
K-평균 군집화(K-means Clustering)
개체들 간 거리가 가까운 것끼리 K개의 그룹을 만드는 군집화의 한 방법
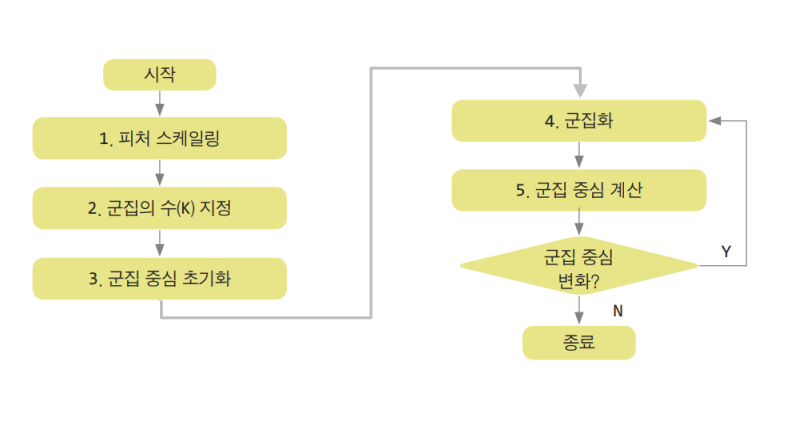
원리
- 클러스터 개수 K 선택
- 임의로 K개의 중심점 초기화
- 각 데이터 → 가장 가까운 중심점에 할당
- 중심점 새로 계산 (평균값)
- 중심점이 더 이상 변하지 않으면 종료
목적함수
\[\min_C \sum_{i=1}^K \sum_{x \in C_i} \|x - \mu_i\|^2\]원리
1 유사도 측정
- 군집 : 개체 간 유사도를 측정하여 유사성이 높은 개체들을 묶은 것
- 유사도 : 군집 중심들과 각 개체 간 유클리드 거리(Euclidean distance)로 측정
- 2차원의 X-Y 평면인 경우, 객체 $s_1 = (x_1, y_1)$와 군집 중심 $\mu_1 = (x_1^c, y_1^c)$간 거리
2 군집화 절차
- 각 군집 중심$(μ_k)$과 그 군집에$(C_k)$ 속하는 개체들과의$(s_i ∈C_k)$ 거리를 최소화하는 방향
① 초기에 개체 1과 2를 군집의 중심으로 정하면, 각 개체들을 가까운 쪽의 군집 중심으로 군집화
② 두 그룹의 각 군집 중심을 다시 정하고, 각 개체들을 재군집
①, ②과정을 반복하다가 군집의 중심이 변하지 않거나, 정해진 반복 수가 되면 종료
장단점
- 장점 :
- 알고리즘이 비교적 간단하고, 수행 속도가 빠르다는 점
- 주어진 데이터에 대한 사전 정보 없이 클러스터링함
- 단점 :
- 클러스터링의 개수 $k$와 최초로 지정하는 중심점들에 따라 결과가 다소 달라질 수 있는 점
- $k$ 사전 지정 필요, 비구형/밀도 불균일·다른 크기 군집에 취약, 이상치 민감
표준 알고리즘
$k$를 결정하는 방법
“팔꿈치 방법”(elbow method)에서는 k를 1부터 증가시키면서 K-means 클러스터링을 수행한다.
각 $k$의 값에 대하여 SSE(sum of squared errors)의 값을 계산한다.
